Real-Time Hand Tracking

Recovering the full articulation of human hands from sensor data is a challenging problem due to the hand’s high number of degrees of freedom, the complexity of its motions, and artifacts in the input sensor data. We investigated various different approaches for hand tracking and developed systems that are capable of real-time posture estimation and tracking of human hands based on RGBD input data.

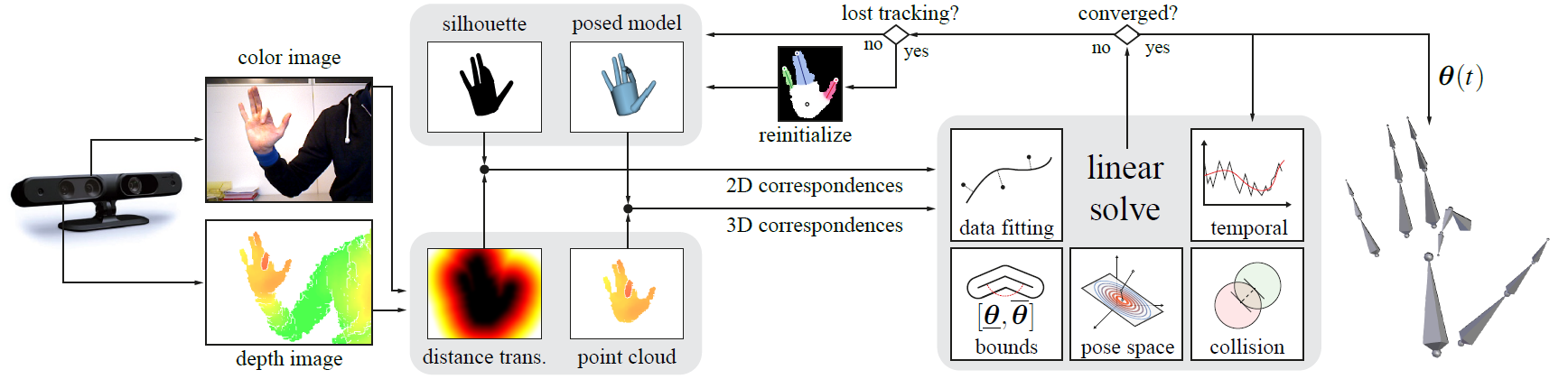
Model-based approaches to hand tracking recover hand movements from RGBD sensors by fitting a virtual hand model to the sensor’s 3D point cloud data [3,5]. Low-cost RBGD devices are easily deployable, but can exhibit strong sensor artifacts (Figure 2). This can lead to errors while computing correspondences between the model and the sensor data. To ensure plausible hand posture reconstructions despite such data flaws, the geometric registration process can be made robust by employing various regularization priors.

**Figure 2:** Data from different RGBD sensors. Top: Intel's Creative Gesture camera (time of flight) provides a complete silhouette image, but low quality depth measurements, resulting in severe point cloud noise. Bottom: point clouds acquired by the PrimeSense Carmine camera (structured light) are much smoother, but the silhouette image can contain significant gaps.

Using robust articulated-ICP [5], hand tracking is formulated as a regularized articulated registration process, in which geometrical model fitting is combined with statistical, kinematic and temporal regularization priors. In this process, an energy encapsulating these combined quantities is minimized in a single linear solve (Figure 3). To account for occlusions and visibility constraints, a registration concept is employed that combines 2D and 3D alignment between the model and the data. 3D point correspondences between the point cloud and the model are computed only with the front-facing parts of the model, which significantly improves the alignment when occlusions occur (Figure 4, Figure 5). In addition to 3D point correspondences, which bring the model close to the data, 2D correspondences between the rendered and sensor silhouettes ensure that the model stays within the visible segment of the hand (Figure 6).

**Figure 3:** Overview of the system in [5]. For each acquired frame a 3D point cloud of the hand and the 2D distance transform of its silhouette is extracted. From these point correspondences are computed to align a cylinder model of the hand to best match the data. This registration is performed in an ICP-like optimization that incorporates a number of regularizing priors to ensure accurate and robust tracking.

**Figure 4:** Illustration of correspondence computations in [5]. The circles represent cross-sections of the fingers, the small black dots are samples of the depth map. (a) A configuration that can be handled by standard closest point correspondences. (b) Closest point correspondences to the back of the cylinder model can cause the registration to fall into a local minimum. Note that simply pruning correspondences with back-pointing normals would not solve this issue, as no constraints would remain to pull the finger towards the data. (c) This problem is resolved by taking visibility into account, and computing closest points only to the portion of the model facing the camera.

**Figure 5:** Illustration of the impact of self-occlusion in correspondences computations in [5]. (a) The finger c2 initially occluded by finger c1 becomes visible, which causes new samples to appear. (b) Closest correspondences to the portion of the model visible from the camera do not generate any constraints that pull c2 toward its data samples. (c) Our method also considers front-facing portions of the model that are occluded, allowing the geometry to correctly register.

**Figure 6:** The 2D silhouette registration in [5] is essential to avoid tracking errors for occluded parts of the hand. When no depth data is available for certain parts of the model, a plausible pose is inferred by ensuring that the model is contained within the sensor silhouette image.

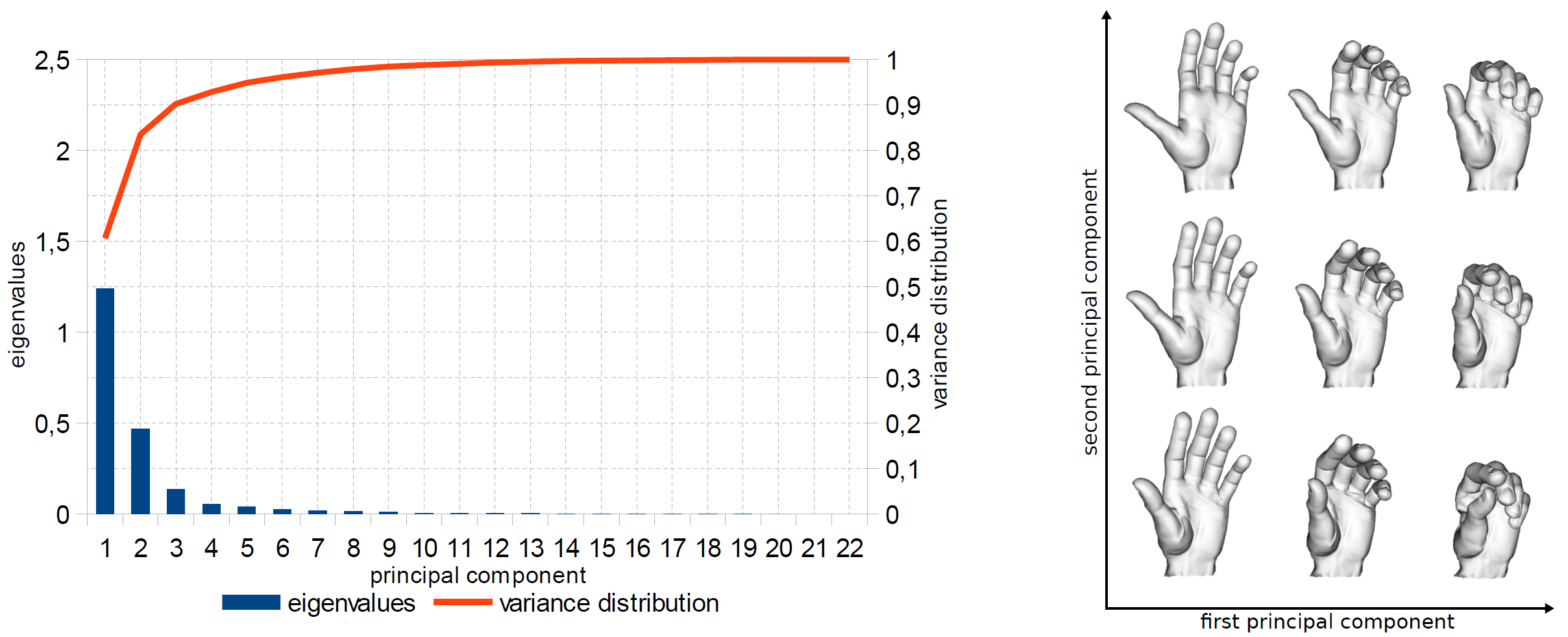
Beyond performing robust correspondence computations and enforcing kinematic constraints, like joint angle limits, temporal coherence and collision detection, statistical analysis of hand motions provides a valuable means of regularizing posture estimations. Performing PCA on a varied dataset of motion captured hand movements exposes the correlations and redundancies present within hand articulations [2,3]. This can be used to derive subspace representations of hand articulations (Figure 7), which can be used to improve the realism of the hand posture estimations in real-time systems when faced with imperfect sensor data [3,5]. The loss of information and flexibility caused by PCA dimension reduction can be compensated for by using an adaptive PCA model [4] that is adjusted during real-time tracking to account for observed hand articulations that are not covered by the initial hand posture parameter subspace.

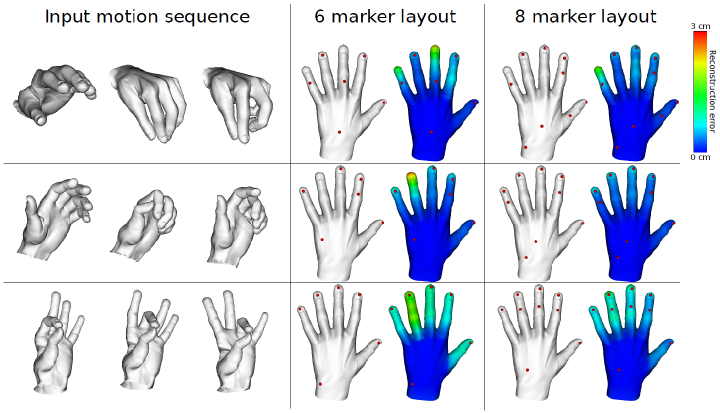
**Figure 7:** PCA of motion captured hand movements [2,3]. Left: eigenvalues and variance distribution among the principal components of a grasping motion data set. The 3 most significant principal components already cover approximately 90% of the data variance. Right: visualization of the degrees of freedom represented by the first and second most significant principal components, which cover about 83% of the data variance and can be used to represent meaningful hand articulations in only two dimensions.

Subspace representations of hand articulations allow for the reconstruction of hand motions from sparse sensor data [3,5]. Conversely, they can also be used to infer the minimal amount of input data necessary for robust hand posture reconstruction in the context of optical motion capture [6,7]. We addressed the problem of determining the optimal placement of a reduced number of markers in order to facilitate accurate posture reconstruction from sparse mocap marker data in a method that automatically generates functional layouts by optimizing for their numerical stability and geometric feasibility (Figure 8).

**Figure 8:** Reduced marker layouts using the method of [6,7]. The input motion sequences are used to automatically determine reduced marker layouts that satisfy numerical stability and geometric feasibility constraints, by optimizing an objective function combining these metrics using stochastic optimization.

In contrast to model-based approaches, which continuously optimize for the kinematic parameters of the hand, appearance-based hand tracking methods produce hand posture estimations from a single frame based on a database of known configurations. We built a system for hand tracking using a color glove [1], which is based on matching the glove-wearing hand’s appearance in the sensor data with an image database (Figure 9), and used it for interactive robot teleoperation (Figure 10).

**Figure 9:** Illustration of the efficient k nearest neighbor search algorithm in [7], which retreives the most similar images to the input in a database based on cascaded image matching. The input image is matched against the database entries in a coarse-to-fine multi-stage hierarchical approach, where the resolution of the images is increased in each stage. The results are k nearest neighbors, whose associated postureq parameters are blended using error-weighted interpolation for the final posture estimate.

**Figure 10:** Application of the hand tracking system in [7] for interactive teleoperation of an anthropomorphic robot hand in a pick-and-place task. This application was carried out in the Bielefeld 'Curious Robot' setup, which has two redundant 7-DoF Mitsubishi PA-10 robot arms each equipped with a 20-DoF Shadow Dexterous Hand.

[1]	Real-Time Hand Tracking with a Color Glove for the Actuation of Anthropomorphic Robot Hands Matthias Schröder, Christof Elbrechter, Jonathan Maycock, Robert Haschke, Mario Botsch, Helge Ritter Proceedings of IEEE-RAS International Conference on Humanoid Robots, 2012, pp. 262-269 Paper Video
[2]	Analysis of Hand Synergies for Inverse Kinematics Hand Tracking Matthias Schröder, Jonathan Maycock, Helge Ritter, Mario Botsch Proceedings of IEEE International Conference on Robotics and Automation (ICRA), Workshop on Hand Synergies, 2013 Paper
[3]	Online Adaptive PCA for Inverse Kinematics Hand Tracking Matthias Schröder, Mario Botsch Proceedings of Vision, Modeling and Visualization, 2014, pp. 111-118. Paper Video
[4]	Real-Time Hand Tracking using Synergistic Inverse Kinematics Matthias Schröder, Jonathan Maycock, Helge Ritter, Mario Botsch IEEE International Conference on Robotics and Automation (ICRA), 2014, pp. 5447-5454. Paper Video Data
[5]	Robust Articulated-ICP for Real-Time Hand Tracking Andrea Tagliasacchi, Matthias Schröder, Anastasia Tkach, Sofien Bouaziz, Mario Botsch, Mark Pauly Computer Graphics Forum 34(5), Proc. Symp. on Geometry Processing, 2015, pp. 101-114. Paper Video Code
[6]	Reduced Marker Layouts for Optical Motion Capture of Hands Matthias Schröder, Jonathan Maycock, Mario Botsch Proceedings of ACM Motion in Games, 2015, pp. 7-16. Paper Video
[7]	Fully Automatic Optical Motion Tracking using an Inverse Kinematics Approach Jonathan Maycock, Tobias Röhlig, Matthias Schröder, Mario Botsch, Helge Ritter Proceedings of IEEE-RAS International Conference on Humanoid Robots, 2015, pp. 461-466. Paper Video
[8]	Design and Evaluation of Reduced Marker Layouts for Hand Motion Capture Matthias Schröder, Thomas Waltemate, Jonathan Maycock, Tobias Röhlig, Helge Ritter, Mario Botsch Computer Animation and Virtual Worlds, 29(6), 2018. Paper Video

Real-Time Hand Tracking

Related Publications