Physically-Based Simulations

Finite element methods are a tremendously important tool for animating scenes showing real-world behavior, for example in virtual reality applications such as surgery simulations, or in computer animation for feature films. In computer graphics, surfaces or solid objects are typically represented by triangle meshes or tetrahedral meshes, respectively. While this allows for simple and efficient simulation codes, dynamically changing the simulation mesh, for instance due to cutting in medical applications or adaptive refinement in complex simulations, requires complex and error-prone remeshing. Our goal therefore is to generalize finite element methods to directly support arbitrary polyhedral elements, which effectively avoids the need for remeshing and thereby simplifies the simulation of fracture or cutting as well as adaptive refinement of the simulation mesh.

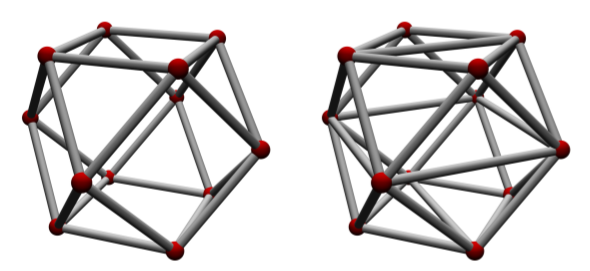
The main challenge is the construction of shape functions for general polyhedral elements that satisfy the requirements of a convergent FEM scheme. In [1] we employ mean-value shape functions, which support convex polyhedral elements with triangulated faces (Figure 1, right). Using harmonic coordinates [3] even allows for non-convex polyhedra and only requires planar faces and linear edges, but not necessarily triangulated faces (Figure 1, left). Another approach is the discontinuous Galerkin method, which allows for discontinuous shape functions by weakly enforcing continuity between elements (Figure 2). This considerably increases the flexibility of the method, and in particular allows arbitrary polyhedra to be simulated [2,5].

**Figure 1:** The general polyhedral element on the left can directly be simulated using harmonic shape functions [3] or discontinuous Galerkin FEM [2]. Mean value shape fuctions [1] require the element's faces to be triangulated (right).

**Figure 2:** Standard, continuous Galerkin FEM stores elastic energy only within elements (left), and the rigid cells of our PriMo framework only use glue-like energies between elements (right). Discontinuous Galerkin FEM (center) employs both types of energies, and can therefore be considered to be a generalization of both methods.

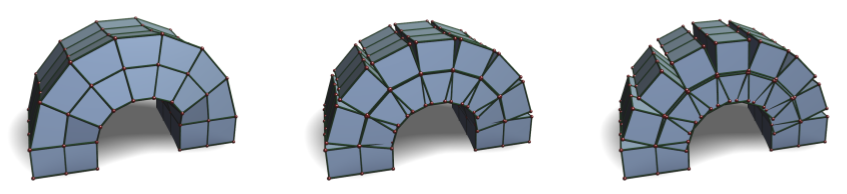
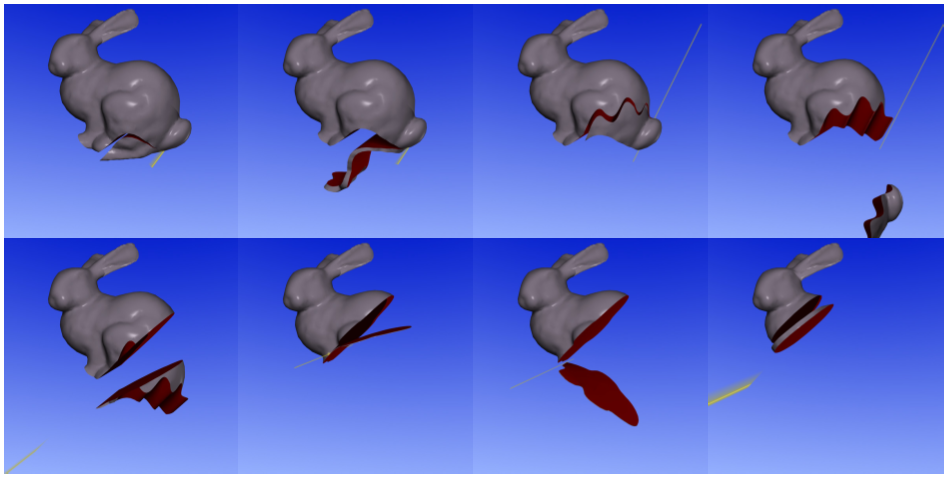
The support for arbitrary polyhedra in FEM schemes significantly simplifies cutting simulations, since the polyhedra resulting from splitting existing elements can directly be simulated without first having to be tessellated into tetrahedra (Figure 3). In comparison to a tetrahedral cutting simulation our method therefore leads to significantly fewer elements (Figure 4). Another application of general polyhedral elements is dynamic, adaptive refinement of the simulation mesh, which allows to spend degrees of freedom where they are most useful (Figure 5). Adaptive refinement leads to hanging nodes or T-junctions, which for many simulation methods require special treatment, but they are directly supported in our polyhedral FEM framework.

**Figure 3:** Supporting arbitrary polyhedra allows to split the two elements as indicated by the blue plane, thereby creating the new red nodes, edges, and faces. The resulting four polyhedral elements can directly be simulated, without the need to first tessellate them into tetrahedra.

**Figure 4:** Several complex cuts through a model consisting of 8k tetrahedra. Standard tetrahedral FEM requires steady remeshing during cutting, resulting in 300k elements in the end. Our polyhedral FEM avoids the complex remeshing and leads to 44k elements only.

**Figure 5:** A bar model (left) is bent (center) and twisted (right). During the dynamic simulation, the hexahedral mesh is adaptively refined using either 1-to-2 splits or 1-to-8 splits, respectively. Thanks to the support for general polyhedral elements the resulting hanging nodes do not require any special treatment.

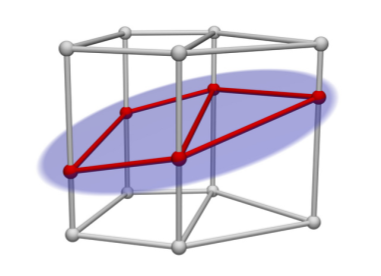
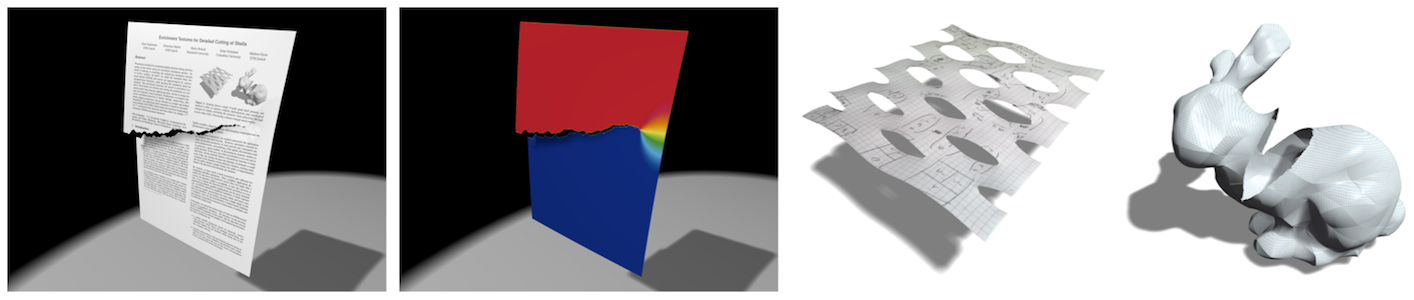
We also presented a method for simulating detailed cutting and fracturing of thin shells using low-resolution simulation meshes [6]. Instead of refining or remeshing the underlying simulation domain to resolve complex cut paths, we adapted the extended finite element method (XFEM) and enrich the set of shape functions by custom-designed basis functions that are discontinuous at the cut location. These enrichment functions are stored in enrichment textures, which allows for fracture and cutting discontinuities at a resolution much finer than the underlying mesh (Figure 6). In order to simulate shells with simple C0-continuous shape functions, which then can easily be enriched by XFEM, we employed Discontinuous Galerkin Kirchhoff-Love shells [4].

**Figure 6:** A single textured quad element being fractured (left), and the underlying discontinuous enrichment function (center-left). Starting from a single quad element, our method is able to capture complex deformations and topological changes by simply enriching the element’s basis functions (center-right). Fracturing a bunny triangle mesh (right).

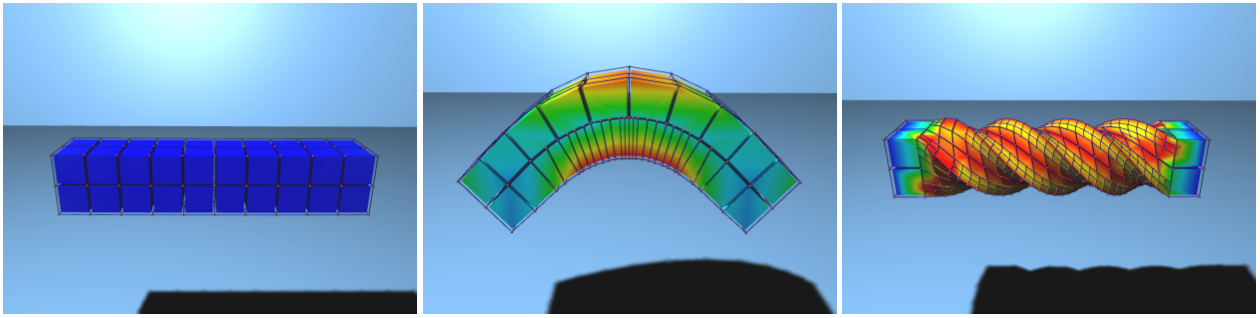
Elastic bodies take many forms, from long and slender rods, to flat and wide shells, to thick and bulky solids. In [7] we developed an accurate, unified treatment of these different types of elastic models. Following the method of resultant-based formulation to its logical extreme, we derived a higher-order integration point, the elaston, that measures stretching, shearing, bending, and twisting along any axis. An assembly of elastons accurately captures the behavior of elastic materials of any dimension. The theory and accompanying implementation do not distinguish between forms of different dimension (solids, shells, rods), nor between manifold regions and non-manifold junctions. Consequently, a single code accurately models a diverse range of elastoplastic behaviors, including buckling, writhing, cutting and merging (Figures 7,8).

**Figure 7:** An elaston measures stretching, shearing, bending, and twisting along any axis (left). An assembly of elastons accurately captures the behavior of elastic materials of any dimension (center), manifold or not, such as this rod cut out of a shell cut out of a cube (right).

**Figure 8:** Elastons accurately reproduce the behavior of elastic shells and rods: The cylinder shows the typicaly buckling patterns as it is getting compressed (left). Twisting a thin rod at both ends generates a plectoneme (center-left). The flag and fish models consist of solid-, shell-, and rod-like parts, whose complex interactions are handled automatically by our unified approach.

[1]	A Finite Element Method on Convex Polyhedra Martin Wicke, Mario Botsch, Markus Gross Computer Graphics Forum 26(3), Proc. Eurographics 2007, pp. 355-364. Paper Video
[2]	Flexible Simulation of Deformable Models Using Discontinuous Galerkin FEM Peter Kaufmann, Sebastian Martin, Mario Botsch, Markus Gross ACM SIGGRAPH / Eurographics Symp. on Computer Animation 2008, pp. 105-115. Paper Video
[3]	Polyhedral Finite Elements Using Harmonic Basis Functions Sebastian Martin, Peter Kaufmann, Mario Botsch, Martin Wicke, Markus Gross Computer Graphics Forum 27(5), Proc. Geometry Processing 2008, pp. 1521-1529. Paper Video
[4]	Implementation of Discontinuous Galerkin Kirchhoff-Love Shells Peter Kaufmann, Sebastian Martin, Mario Botsch, Markus Gross Technical Report No. 622, ETH Zurich, 2009. Paper
[5]	Flexible Simulation of Deformable Models Using Discontinuous Galerkin FEM Peter Kaufmann, Sebastian Martin, Mario Botsch, Markus Gross Graphical Models 71(4), 2009, pp. 153-167. Paper Video
[6]	Enrichment Textures for Detailed Cutting of Shells Peter Kaufmann, Sebastian Martin, Mario Botsch, Eitan Grinspun, Markus Gross ACM Trans. on Graphics 28(3), SIGGRAPH 2009, pp. 50:1-50:10. Paper Video
[7]	Unified Simulation of Elastic Rods, Shells, and Solids Sebastian Martin, Peter Kaufmann, Mario Botsch, Eitan Grinspun, Markus Gross ACM Trans. on Graphics 29(4), SIGGRAPH 2010, pp. 39:1-39:10. Paper Supplementary Material Video Supplementary Video

Physically-Based Simulations

Related Publications